Euler’s Number

2.718281828459045235360287…

I’ve come across the value ‘e’ many times before; it’s one of those particular numbers that we hear mathematicians speak about quite frequently, especially in the case of Euler’s Identity, which is nicknamed the most beautiful formula in mathematics. But I realised that I know very little about what the number really represents. So what really is this famous e and what is its significance?

Imagine you start off with 1 dollar, and you receive 100% compound interest every year, then after 1 year, you would have gained 1 dollar. Your total would be 2 dollars.

If you start off with 1 dollar and gain 50% compound interest every 6 months, that value would increase to 2.25 dollars after a year.

And so on… the more frequently you obtain your compound interest, the higher your value is by the end of the year.

So, Euler asked the question: what would the value be if we did this every instant? And he found out that the answer was 2.71828… a never-ending irrational number.

He calculated the first 18 decimals using the formula:

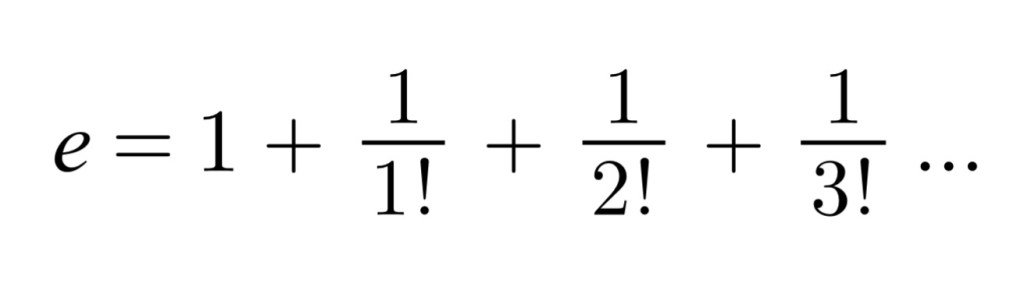
Well, alright, sounds cool and all, but I’m still wondering, what’s so special about this number?

Mathematicians call e the natural language of calculus, and there’s a reason why. Let’s take a look at the graph of e^x…

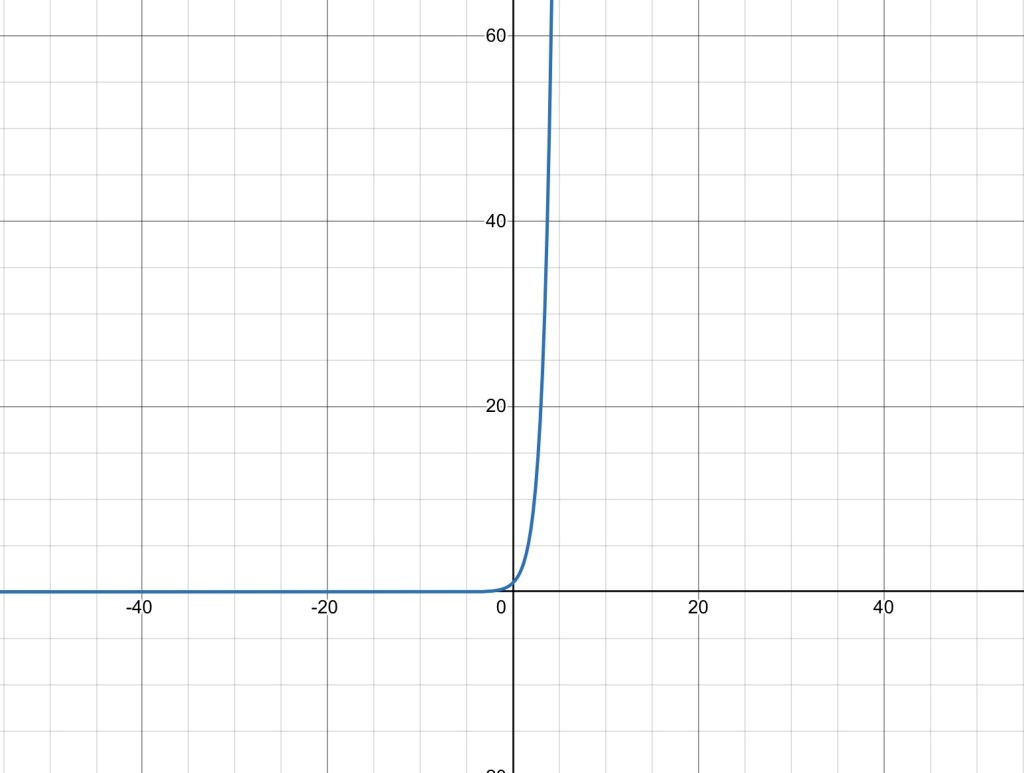
At first, we notice some relatively obvious points:

• This is the graph of an exponential function
• The y-intercept must be at (0,1)
• As x approaches –∞, e^x approaches zero, meaning the value gets smaller and smaller but never reaches 0.
• As x approaches ∞, e^x also goes to infinity, meaning the value gets bigger and bigger.

However, there’s something which makes this graph particular. With most other graphs, the gradient of the curve at any point (its derivative) is different to the function itself. For example, derivative of the function y=x^2 is 2x. However, in the case of e^x, the derivative of the function is e^x itself… therefore the gradient of the graph at each point is equal to the y value of that point.

This implies that the gradient of the function is proportional to its height, or in simpler terms, the higher the function goes, the faster it rises.

This is quite significant, because it models systems where growth or decay depends on the current amount, such as population growth (the more people there are, the faster the population grows) and radioactive decay (the less radioactive material remaining, the slower the decay rate becomes).

The graph of e^x models the growth and decay we see in nature with unparalleled elegance.