In the early 1900s, a young woman named Amalia Emmy Noether made the—highly unconventional decision at the time—to study academics in the University of Erlangen. I say this was highly unconventional because it was a time when educating women in traditionally male-pursuits was seen as a recipe for “overthrowing all academic order.” In fact, Noether was one of only two women in the university of around 1000 students, and instead of being able to participate in classes she was only permitted to audit lectures.
Despite these odds, Noether would become one of the great mathematicians of history, and her discoveries would become essential to both physics and mathematics. One of such discoveries was her theory of symmetries in nature, now referred to as Noether’s Theorem.
Noether’s theorem states that for every symmetry in nature, there is a corresponding conservation law, and for every conservation there must be a symmetry involved.
You might be familiar with conservation laws from Highschool physics: the conservation of energy, the conservation of momentum… etc. In simple terms, conservation laws indicate that in an isolated system, there are certain quantities which do not increase or decrease: they always stay the same.
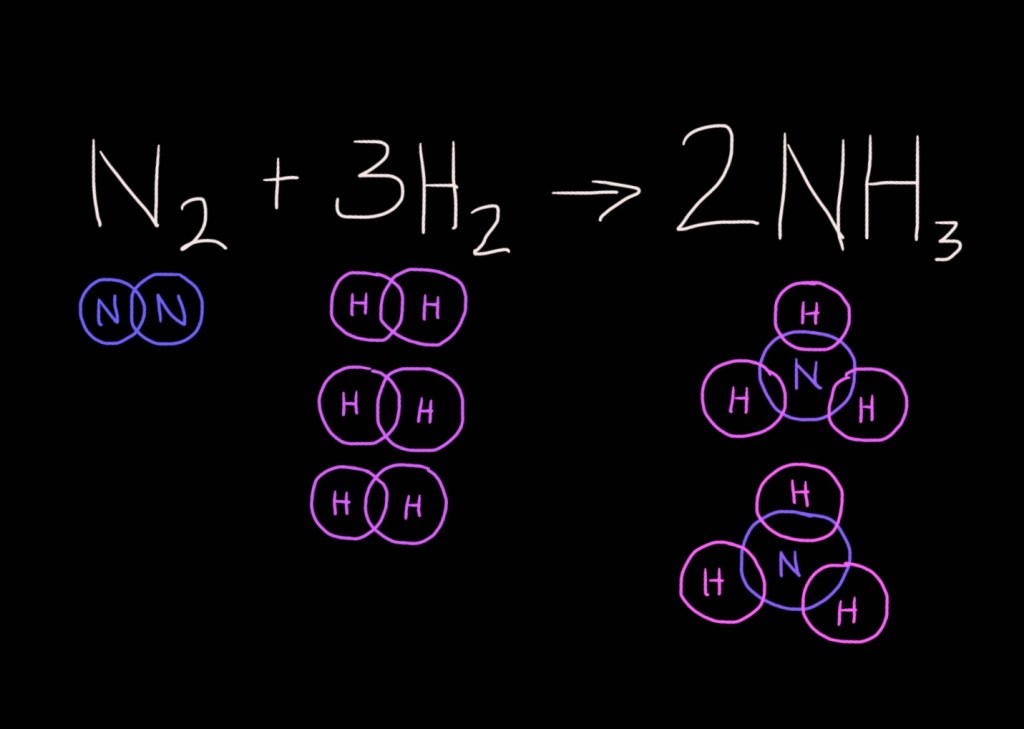
For example, in a chemical reaction, the number of reactant atoms must be equal to the number of product atoms, because mass is conserved (atoms cannot be created out of nowhere mid-way through the reaction!)
What Noether discovered was that there is connection between symmetry and conservation.
—————————————————
- Conservation of Energy
If I were to throw a ball and record its movement, then throw the ball again a month later (ie, forward in time) I will record the exact same observations.
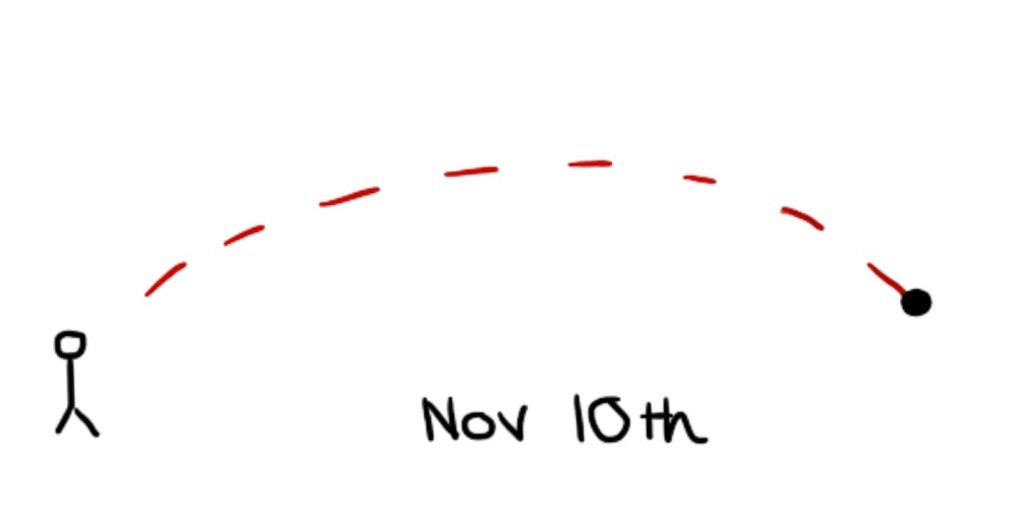
The laws of physics that apply to the ball I threw on November 10th are identical to the ones that apply on December 10th.
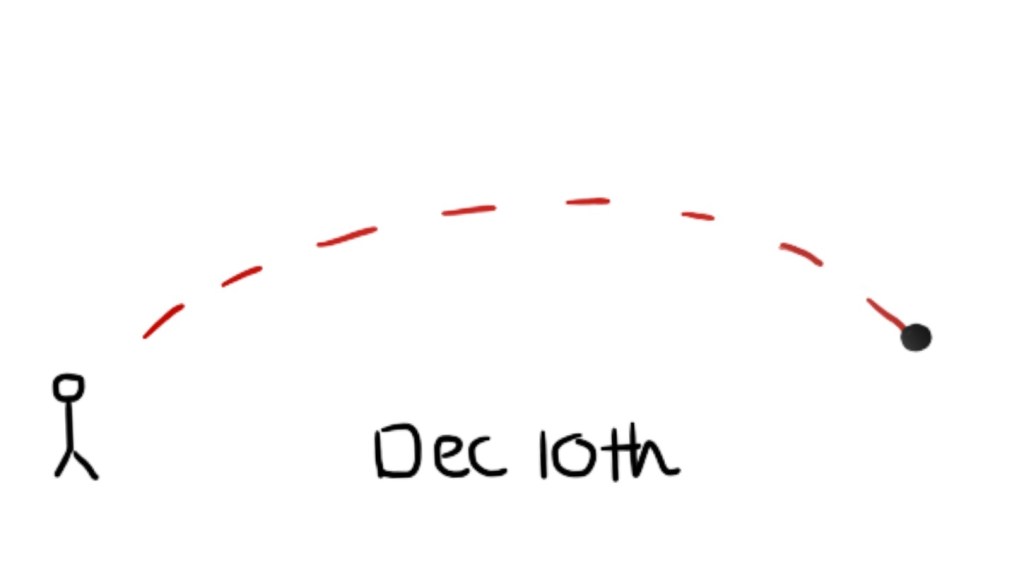
There is a symmetry in translation through time… and this symmetry, Noether found, indicates a conservation in energy.
2. Conservation of Momentum

Similarly, if we choose our system to be a planet orbiting a star, and we move the star and the planet in space however far we want, the same laws of physics will apply and will act the same way.
This is an example of translational symmetry, and it indicates that momentum is conserved.
3. Conservation of Angular Momentum
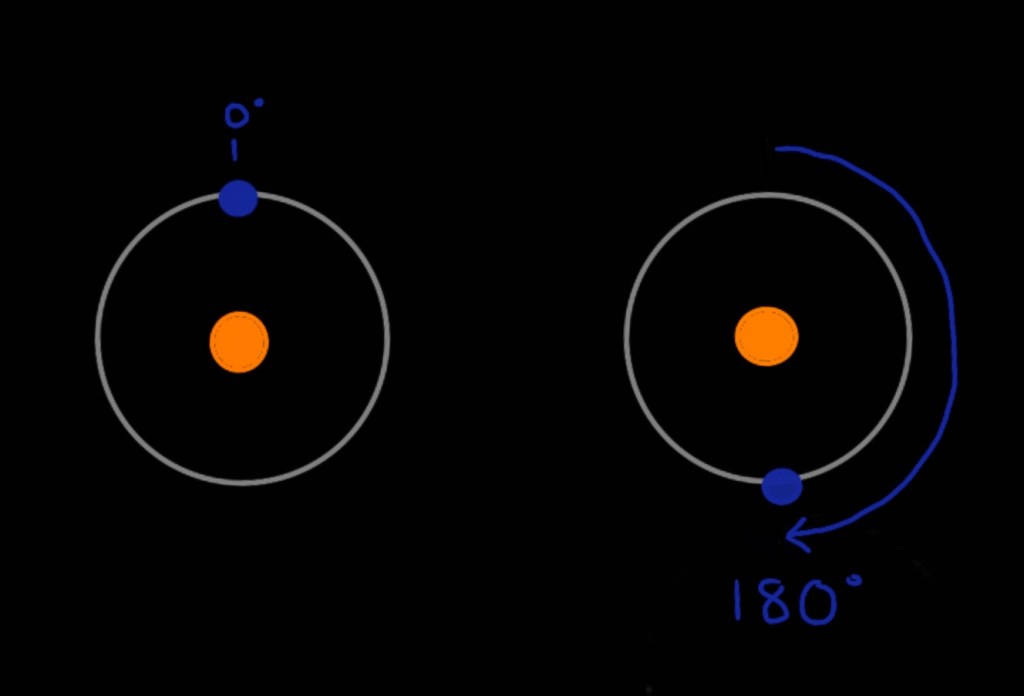
As well as that, if we assume the planet begins its orbit around the star in a certain position, and we rotate the planet 180 degrees ahead, the same laws of physics will apply and produce the exact same observations.
This indicates a conservation in angular momentum.
What makes Noether’s theorem so significant is that it tells us when conservation laws apply and when they don’t. Let’s take an example of a ball falling towards the ground: a ball at 50m above ground will have more gravitational potential energy than a ball at 5m above the ground. Therefore, if we drop ball from a shorter height, it will not result in a translational symmetry, and because of this, the conservation of momentum does not apply here.
——————————————
Noether’s work was mainly spread by her male colleagues, such as mathematicians David Hilbert and Felix Klein, and for a long time, she did not gain the recognition she deserved. Nonetheless, her theorem was recognised by the great mathematicians and physicists of the time because it had significant implications on their own work. In the words of the German physicist Hermann Weyl, “Miss Noether discovered the connection between invariance and conservation. That is a result of great beauty, and a great contribution to physics.”
Leave a comment