Proof 1 of Pythagoras’ Theorem

We’ve all come across the legendary Pythagoras’ Theorem in Highschool geometry: a theorem which states that in a right angled triangle, the length of the hypotenuse (squared) is equal to the length of the opposite (squared) plus the adjacent (squared), or in more familiar terms:

c² = a² + b²

There are over 600 ways to prove this theorem. Here is one…

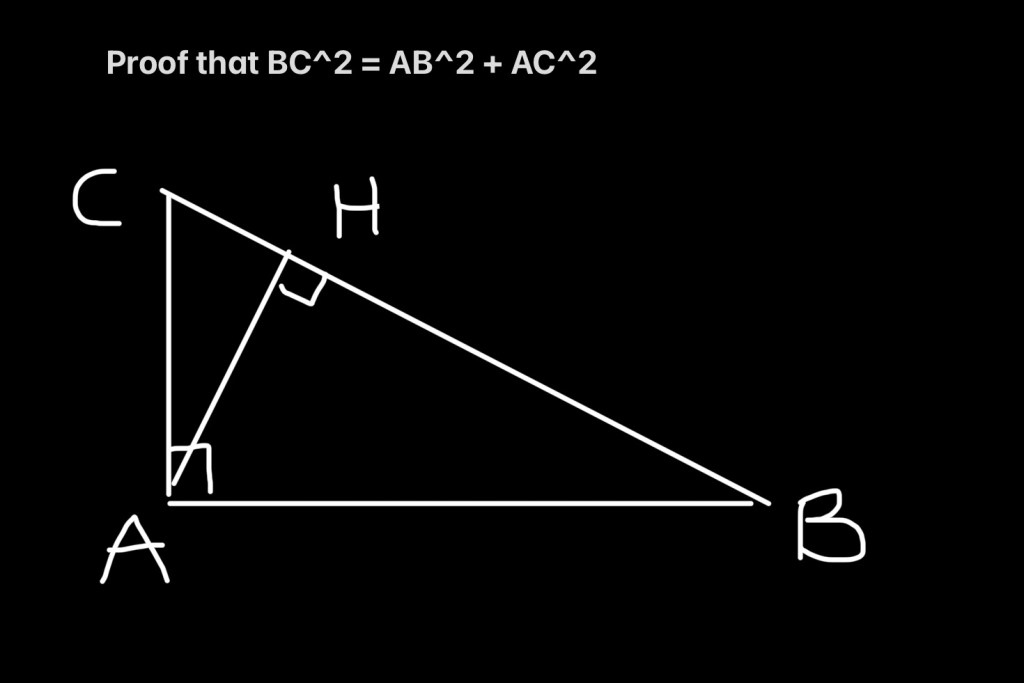
In this example:

• CAB is a right angled triangle.
• AH is the perpendicular projection of A onto CB
• Therefore, BC corresponds to the hypotenuse, while AB and AC correspond to ‘a’ and ‘b’ in our initial formula.

So let the proof begin…

1. We know that triangle CAB is similar to AHB and AHC because:
   • Triangles CAB and AHB both have a right angle and angle ABH in common (two equal angles is enough to prove two triangles are similar, since from two angles you can find the third and show that all angles are equal.)
   • Triangles CAB and AHC both have a right angle and angle ACH in common.
2. This means that:
   • k = AC/HC = CB/AC —> AC^2 = BC x HC
   • k = AB/CB = HB/AB —> AB^2 = BC x HB
3. AC^2 + AB^2 = BC x HB + BC x HC
   • AC^2 + AB^2 = BC (HB + HC)
   • And because, by looking at the diagram, HB + HC = BC, we come to the conclusion that: AC^2 + AB^2 = BC^2

QED